W/Z classification

Estimated reading time: 2 minutes

Introduction

  • When z and w all decay to quarks, and these quarks will hadronization. We want to classify w and z through using the information of their decay products. In this experiment, we will use the four momentum of quarks decayed from w or z to classify w and z.

Method

There are two ways to use the information of four momentum of quarks:

  • Using the information of invariant mass calculated through correctly pairing two quarks among four quarks decayed from two w or z bosons. We all know the rest-mass of w and z is 80Gev and 91Gev separately. So the value of invariant mass will help us classify w and z.
  • Using deep-neural-network to classify w and z.

Samples:

  • For this exprement, the w and z boson are product from the collision of position and electron, it is in generation level, not through simulation or reconstruction. The channels we use are as following table:

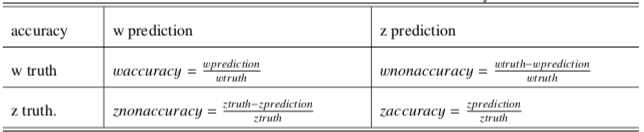
The definition of accuracy

  • We want to classify w and z by two ways independently, so need to make a rule to compare the classification result of these two ways. In this experiment, we use the following rule: Assumpt the number of w and z boson is wtruth and ztruth separately, through the way of invariant mass or deep learning, correctly classifying the number of w and z boson is wpre and zpre separately, since that there are two classes, so the incorrectly classifying number of w and z boson is (wtruth-wpre) and (ztruth-zpre) separately. The definition is as following table:

Invariant-mass method

  • Since the charge of z and w boson is zero and one separately. We can use this character to correctly pairing quarks to calculate invariant mass. The following graph is the distribution of invariant mass of w and z:

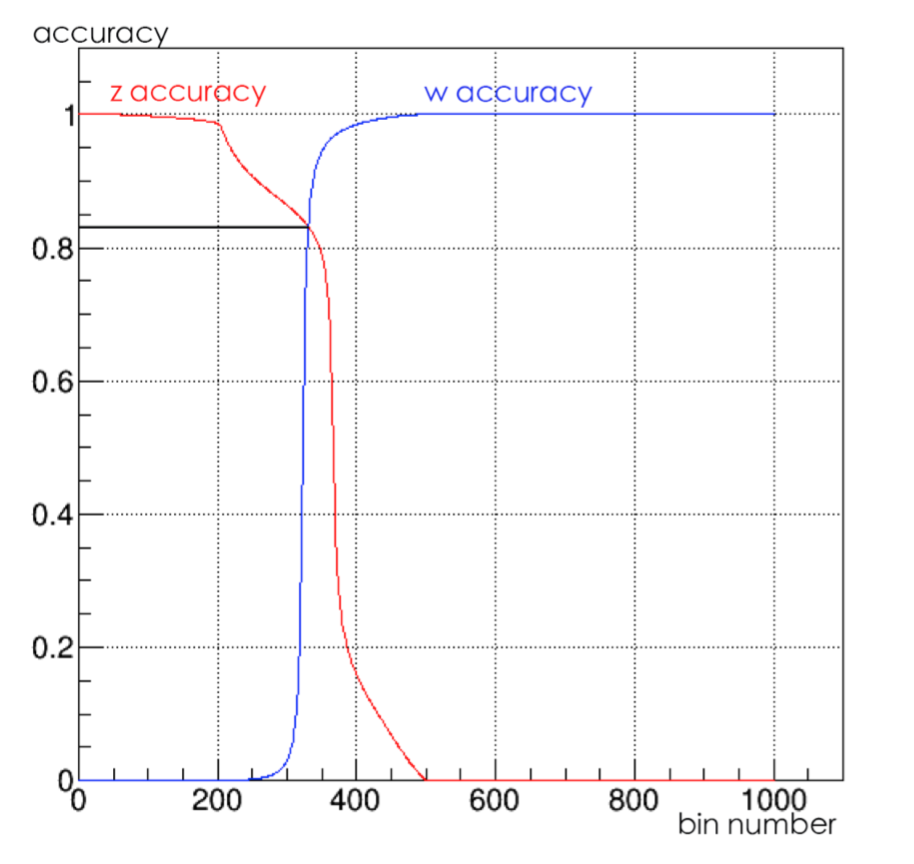
  • The following graph is the classification accuracy:

Deep-learning method

  • We all know deep-learning is powerful. For out problem, the convolution-neural-network and recurrent-neural-network don’t work well since there is no structure information or sequential information, so we decide to use deep-neural-network to classify w and z boson.
  • The samples are divided into three sets: training set, validation set and testing set. For out experiment, there are 600000 samples in training set, 100000 samples in validation set and 80000 samples in testing set.
  • Each sample have several features, the concrete number and type of features is due to our selection. These features will help us to classify w and z.
  • The structure of DNN model is shown in http://cepcgit.ihep.ac.cn/zhuyongfeng/ee_zz_vvqq.

Deep-learning result

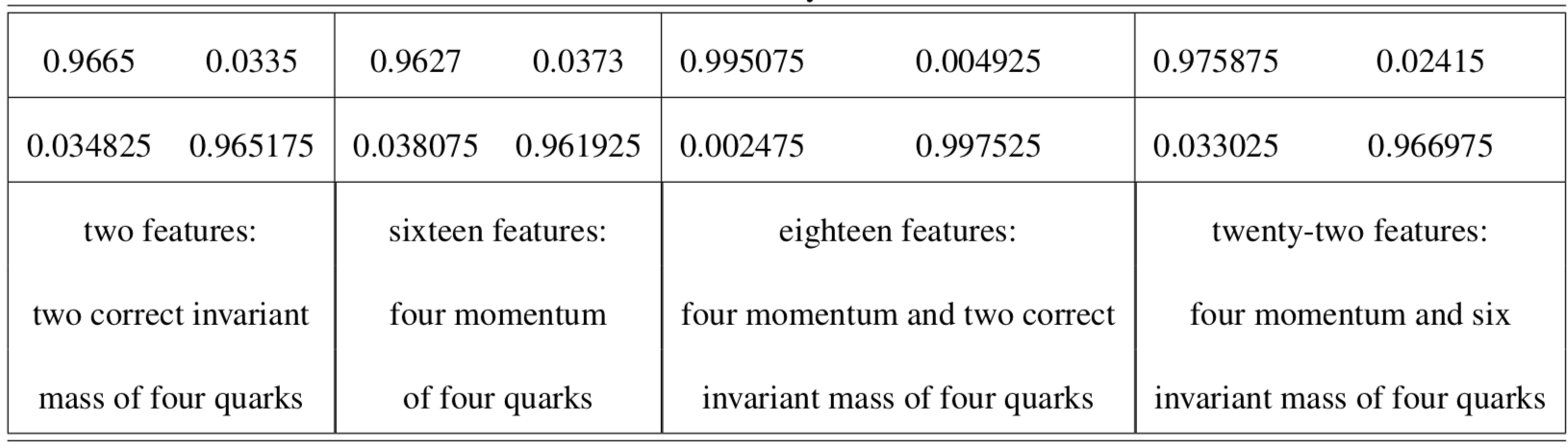
  • There are four conditions as show in following table as well as their classification result:

Conclusion

  • You have to say that deep-learning is powerful.